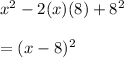Question

. Complete the square for x 2 − 16x + __ .

Then write the resulting expression as a binomial squared.
a. −64; (x + 8) 2

b. −64; (x − 8)

c. 64; (x − 8) 22

d. 64; (x + 8) 2

Answer 1

Correct Answer: Option C

The given expression is:


`x^(2) -16x`

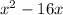
The formula for complete square is:


`(a-b)^(2) = a^(2) -2ab+ b^(2)`

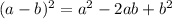
The given expression can be re-written as:


`x^(2) -2(x)(8)`

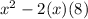
So, we have the square of first term which x and twice the product of first and second term x and 8. What is missing is the square of second term. Second term is 8. So square of 8 which equals 64 is missing.

Therefore, complete square will be:


`x^(2) -2(x)(8)+ 8^(2) \\ \\ =(x-8)^(2)`