Question

What transformation has changed the parent function f(x) = log4x to its new appearance shown in the graph below?

Answer 1

`f(x)=-\log_4x`

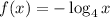
Explanation:

Given :
`f(x)=\log_4x`

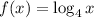
To find : What transformation has changed to the parent function f(x) to its new appearances.

Solution :

First we plot the graph of
`f(x)=\log_4x`

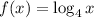
→ (Graph attached below)

We see that the graph we get that there is a reflection over x-axis.

Reflection over x-axis :

If line y=x then reflection over x-axis is x-coordinate and y-coordinate change places y=-x and x-coordinate change its sign.

The new transformation is
`f(x)=-\log_4x`.

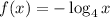Both function is mapped graphically below.

Answer 2

The shape of this graph is clearly a reflection of normal log function by x axis. So the first step is to reflect log4x by x axis. When x=4, log4x=1, but in this case, the function is equal to 2 (after reflection). So the graph must have been stretched by a factor of 2 along y axis, which is the second step.