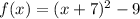Question

Given ​ f(x)=x2+14x+40.
Enter the quadratic function in vertex form in the box.

Answer 1

For this case we have an equation of the form:

`y = ax ^ 2 + bx + c`
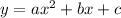
This equation in vertex form is:

`f (x) = a (x - h) ^ 2 + k`
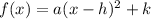
where (h, k) is the vertex of the parabola.
We have the following function:

`f (x) = x ^ 2 + 14x + 40`
We look for the vertice.
For this, we derive the equation:

`f '(x) = 2x + 14`
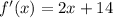
We equal zero and clear the value of x:

`2x + 14 = 0 2x = -14 x = -14/2 x = -7`
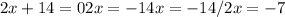
Substitute the value of x = -7 in the function:

`f (-7) = (- 7) ^ 2 + 14 * (- 7) +40 f (-7) = -9`
Then, the vertice is:

`(h, k) = (-7, -9)`
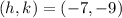
Substituting values we have:

`f (x) = (x + 7) ^ 2 - 9`
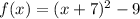Answer:
The quadratic function in vertex form is:

`f (x) = (x + 7) ^ 2 - 9`