Let's make this simple. Let's have the small cone have a radius 1 and the height 1. This would make the bigger
cone
have a radius of 1 and the height of 2.
With this information, lets get the volume of both cones. The formula is this:
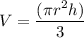
Plug in numbers:
Small cone:

Big cone:
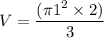
The small cone has a volume of

The big cone has a volume of
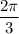
Now, you want to find how many small cones you need to have the same total volume of the big cone.
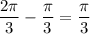
You have the difference of pi over 3 comparing the big cone to the small one. You realize that the small cone has the same volume of that. Therefore,
you need 2 small cones to have the same total volume as the larger cone