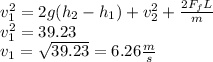Question

You are riding on a roller coaster that starts from rest at a height of 25.0 m and moves along a frictionless track. however, after a bad storm some leaves settled on part of the track causing a 9.4-m length of the track to exert a frictional force of 625 n on the car. to safely make it around the loop, the 50-kg car must have a minimum speed of 7.7 m/s at the top of the loop (point b). how fast should the car be moving initially at point a to ensure that it reaches the top of the loop with the minimum required speed?

Answer 1

speed at initial point A must be v = 6.3 m/s

Step-by-step explanation:

Here we know that the speed of car at point B must be 7.7 m/s

now by energy conservation we know that total mechanical energy at point B is given as

`E_2 = (1)/(2)mv_2^2 + mgh_2`

`E_2 = (1)/(2)(50)(7.7)^2 + (50)(9.8)(12)`

`E_2 = 7362.25 J`

Now let say the initial speed at point A is v so initial total energy is given as

`E_1 = (1)/(2)m_1v_1^2 + mgh_1`

`E_1 = (1)/(2)(50)v_1^2 + (50)9.8(25)`

`E_1 = 25v_1^2 + 12250`

now we know that here energy is lost due to friction which is given by work done by the friction

`W_f = f.d`

`W_f = (625)(9.4) = 5875J`

now we know that

energy loss = E1 - E2

`5875 = (25 v_1^2 + 12250) - 7362.25`

by solving above equation we have

`v_1 = 6.3 m/s`

Answer 2

I attached the missing picture.
We can figure this one out using the law of conservation of energy.
At point A the car would have potential energy and kinetic energy.

`A: mgh_1+(mv_1^2)/(2)`
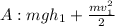
Then, while the car is traveling down the track it loses some of its initial energy due to friction:

`W_f=F_f\cdot L`
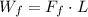
So, we know that the car is approaching the point B with the following amount of energy:

`mgh_1+(mv_1^2)/(2)- F_fL`
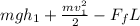
The law of conservation of energy tells us that this energy must the same as the energy at point B.
The energy at point B is the sum of car's kinetic and potential energy:

`B: mgh_2+(mv_2)/(2)`
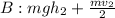
As said before this energy must be the same as the energy of a car approaching the loop:

`mgh_2+(mv_2)/(2)=mgh_1+(mv_1^2)/(2)- F_fL`
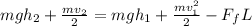
Now we solve the equation for
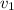
`v_1`:

`v_1^2=2g(h_2-h_1)+v_2^2+(2F_fL)/(m)\\ v_1^2=39.23\\ v_1=√(39.23)=6.26(m)/(s)`