Answer:
Current, I = 1.35 A
Step-by-step explanation:
Given that,
Resistance of circuit, R = 30 ohms
Power of the circuit, P = 55 W
The power in a light bulb is given by the equation is :
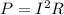
I is the current in a circuit
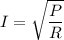

I = 1.35 A
So, the current in a circuit is 1.35 A. Hence, this is the required solution.