First, we are going to find the difference,

, of our sequence. Remember that in an arithmetic sequence

, so:
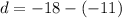
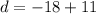
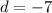
Now that we have our difference, we can find the sum of the first 14 terms of our sequence using the formula:
![S_(n)= (n)/(2) [2a_(1)+(n-1)d]](https://img.qammunity.org/2019/formulas/mathematics/high-school/rprieltmvgp36hc9yptzy24fr25fo2hfto.png)
where

is the number of terms we want to add
We now know that
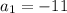
,
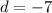
, and
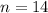
. So lets replace those values in our formula:
![S_(n)= (14)/(2) [2(-11)+(14-1)(-7)]](https://img.qammunity.org/2019/formulas/mathematics/high-school/k8uw0n2l2tscvsbfw2bvb6dkv5ztcje7pg.png)
![S_(n)=7[-22+(13)(-7)]](https://img.qammunity.org/2019/formulas/mathematics/high-school/pa3xqef2hm3cfnwv1868nb75mditeq637u.png)


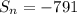
We can conclude that the sum of the first 14 terms of our sequence is
-791.