Question

The sides of an equilateral triangle are 8 units long. What is the length of the altitude of the triangle?

Answer 1

`\bf \textit{height of an equilateral triangle}\\\\ h=\cfrac{s√(3)}{2}\qquad \begin{cases} s=\textit{length of a side}\\ ---------\\ s=8 \end{cases}\implies h=\cfrac{8√(3)}{2}`

Answer 2

Answer: The answer is 4√3 units.

Explanation: As shown in the attached figure, ABC is an equilateral triangle with AB = BC = CA = 8 units and AD is the altitude.

We know that every altitude of an equilateral triangle divides the opposite side in two equal parts.

So, in ΔABC, we have

BD = DC = half of BC.

So,

`BD=DC=(8)/(2)=4~\textup{units}.`

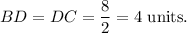
Since AD is perpendicular to BC, so ΔABD will be aright-angled triangle.

Using Pythagoras Theorem, we can write

`AB^2=AD^2+BD^2\\\\\Rightarrow 8^2=AD^2+4^2\\\\\Rightarrow 64=AD^2+16\\\\\Rightarrow AD^2=64-16\\\\\Rightarrow AD^2=48\\\\\Rightarrow AD=4\sqrt 3.`

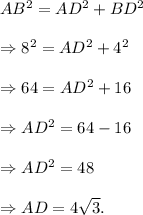
Thus, the length of the altitude is 4√3 units.