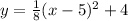Question

What is the equation of the quadratic graph with a focus of (5, 6) and a directrix of y = 2? f(x) = one eighth (x + 5)2 + 4 f(x) = −one eighth (x − 5)2 + 4 f(x) = one eighth (x − 5)2 + 4 f(x) = one eighth (x + 5)2 − 4

Answer 1

In this problem, given the focus at (3, 1) and directrix at y = 5, then it is implied that the parabola is facing upwards. The vertex hence is at the middle of the focus and the directrix, hence at (3, 3). The general formula of the parabola is y-k = 4a ( x-h)^2. Substituting, y - 3 = 1/8 *(x-3)^2.

Answer is A

Answer 2

`y=(1)/(8) (x-5)^2 + 4`

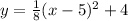
Explanation:

the equation of the quadratic graph with a focus of (5, 6) and a directrix of y = 2

General equation of a parabola in vertex form is

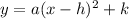`y=a(x-h)^2 + k` , where (h,k) is the vertex

The distance between focus and directrix is 2p

focus of (5, 6) and a directrix of y = 2

distance is 4

2p = 4 so p = 2

Vertex is the midpoint of focus and directrix that is (5,4)

h= 5 and k= 4

Now find out 'a' , a=
`(1)/(4p)`

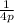
a=
`(1)/(y4(2)) =(1)/(8)`

`y=(1)/(8) (x-5)^2 + 4`