Question

Derive the equation of the parabola with a focus at (–5, –5) and a directrix of y = 7. (2 points)

f(x) = (x + 2)2 + 3/4

f(x) = –(x + 2)2 – 3/4

f(x) = –(x – 2)2 + 3/4

f(x) = –(x – 2)2 – 3/4

Answer 1

We will use vertex form of the parabola:

`y=a(x-h)^2+k`
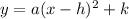
Where (h,k) is the vertex of our parabola. We know that focus and directrix are located at the same distance from the vertex. That distance is a.
We can use this to build a system of equations to calculate a and k. We already know that h=-5, keep in mind that focus and vertex share the same x coordinate.

`7=k-a\\ -5=k+a`
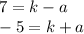
We just add these two equations together:

`2=2k\\ k=1`
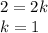
We plug this back into the first equation:

`7=1-a\\ a=-6`
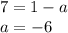
That's all the information we need to write down the equation:

`y=-6(x+5)^2+1`
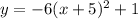
None of the answers you provided are correct.