Question

Suppose the number of gallons of gasoline per day used by a car is normally distributed with a mean of 2.2 gallons and a standard deviation of 1.2 gallons.

What is the difference in gallons per day used by a car with a z-score of 3 and another car that has a z-score of 0?

A. 1.2

B. 2.6

C. 3.6

D. 4.6

Answer 1

The difference in gallons per day used is 3.6.

The formula to calculate a z-score is:

`z=(X-\mu)/(\sigma)`,

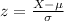
where X is the value used to calculate the score, μ is the mean and σ is the standard deviation. We have the z-scores so we must work backward:


`3=(X-2.2)/(1.2)\text{ and }0=(X-2.2)/(1.2)`

For both equations, we will cancel the 1.2 by multiplying both sides:

`3*1.2=((X-2.2)/(1.2))*1.2\text{ and }0*1.2=((X-2.2)/(1.2))*1.2 \\ \\3.6=X-2.2\text{ and }0=X-2.2`

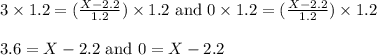
Now we will cancel 2.2 from both equations by adding it to both sides:

3.6+2.2=X-2.2+2.2 and 0+2.2=X-2.2+2.2
5.8=X and 2.2=X

The difference in gas used per day would be given by
5.8-2.2 = 3.6.