Question

D^2+d-30/d^2+3d-40 + d^2+14d+48/d^2-2d-48

A. D^2+14d+16/(d+8)(d-8)
B. 2d^2+14d+16/(d+8)(d-8)
C.2d^2+15d+18/2d^2+d-88
D.2d^2+15d+18/(d+8)(d-8)

Answer 1

I think D.2d^2+15d+18/(d+8)(d-8)

Answer 2

Answer: option B.

2d^2 + 14d + 16
----------------------------
(d+8)(d-8)


Step-by-step explanation:

The question is:


`(d^2+d-30)/(d^2+3d-40) + (d^2+14d+48)/(d^2-2d-48)`

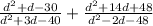
1) Start factoring all the polynomials to rewrite the fractions.

2) d^2 + d - 30 = (d + 6)(d - 6)

3) d^2 + 3d - 40 = (d + 8)(d - 5)

4) d^2 + 14d + 48 = (d + 6) (d + 8)

5) d^2 - 2d - 48 = (d - 8)(d + 6)

6) rewrite the fractions:

(d+6)(d-5) (d+8)(d+6)
----------------- + -----------------
(d+8)(d-5) (d-8)(d+6)

7) simplify the fractions cancelling the factors that are equal in the numerator and the denominator:

d+6 d+8
-------- + -------
d+8 d-8

8) take least common denominatior: (d+8)(d-8), and sum the fractions:

(d-8)(d+6) + (d+8)^2
--------------------------------
(d+8)(d-8)

9) expand the parenthesis in the numerator and combine like terms:

d^2 - 2d - 48 + d^2 + 16d + 64
------------------------------------------- =
(d+8)(d-8)

2d^2 + 14d + 16
= ----------------------------
(d+8)(d-8)

And that is the option B.