Question

Explain how you can determine that the following system has one unique solution – without actually solving the system. 2x+y=4 , 2y=6-2x

Answer 1

Both equations has different slope , so the system of equation have one unique solution.

Explanation:

`2x+y=4` ,
`2y=6-2x`

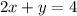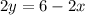
To determine that the system of equation has unique solution, we need to find out the slope.

To find slope, we write the equation in the form of y=mx+b

Where m is the slope and b is the y intercept

`2x+y=4`

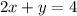
Subtract 2x on both sides

`y=-2x+4`

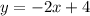
here, m= -2 is the slope

`2y=6-2x`

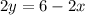
Divide both sides by 2

`y=3-x`

`y=-x+3`

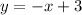
Slope m = -1

Both equations has different slope , so the system of equation have one unique solution.

Answer 2

Answer: The slopes are different

To compare the lines put them both in slope intercept form. The first equation will be y = -2x + 4 and the second equation will be y = -1x + 6. The slopes of the 2 graphs are different. These means that they are going in different directions. Therefore, they will cross a one unique point.