Question

If the circle x2 - 4x + y2 + 2y = 4 is translated 3 units to the right and 1 unit down, what is the center of the circle?

Answer 1

The correct answer is (5,-2).

I took the test

Answer 2

(5,-2).

Explanation:

First, let's find the original center of the circle, we have

`x^2 - 4x + y^2 + 2y = 4`

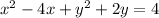
we are going to complete square adding and subtracting 4 for the x terms and 1 for the y terms

`x^2 - 4x+4-4 + y^2 + 2y+1-1 = 4`

`(x-2)^2 - 4 + (y+1)^2 - 1 = 4`

`(x-2)^2+ (y+1)^2 - 5 = 4`

`(x-2)^2+ (y+1)^2 = 4+5`

`(x-2)^2+ (y+1)^2 = 9.`

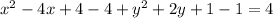
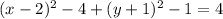
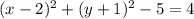
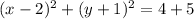
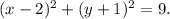
The canonical formula of a circumference is
`(x-h)^2+(y-k)^2=r^2`

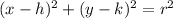
Then, we have a circle with
`r^2 =9` and center (h,k)=(2,-1).

Now, if we translate the circle 3 units to right and 1 unit down, then all the points in the circle will be translated including the center. Especifically, the x values will be added 3 units and the y-vaues will be subtracted 1 unit, then the new center will be

(2+3,-1-1) = (5,-2).