When factoring an expression, we need to identify the Greatest Common Factor of the expression (GCF). By definition, GCF is the product of prime factors involved with its Lowest Exponent.
We need to divide each term by the GCF to get the expression inside the parenthesis.
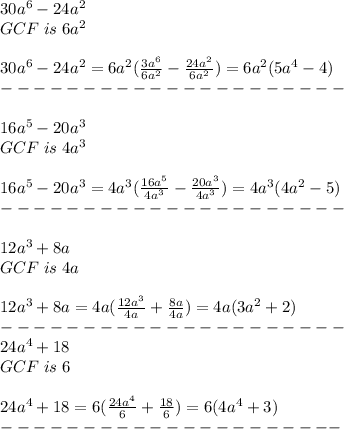
Conclusion:
From above we can conclude that the below expressions are factored completely
