we are given
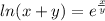
Since, we have to solve for dy/dx
so, we will take derivative with respect to x on both sides
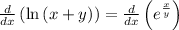
Left side:
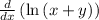
we can use chain rule
u=x+y
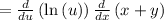
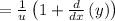
now, we can plug back
u=x+y
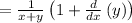
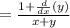
Right side:

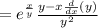
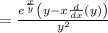
now, we can set them equal
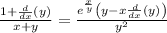
now, we can solve for dy/dx
we get
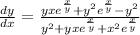 ..............Answer
..............Answer