Question

At the avonlea country club, .73 of the members play bridge and swim, and .82 play bridge. if a member is selected at random, find the probability that the member swims, given that the member plays bridge.

Answer 1

0.89.

Explanation:

We have been given that at the Avonlea country club, 0.73 of the members play bridge and swim, and 0.82 play bridge.

To find the probability for our given problem we will use conditional probability formula.

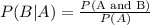`P(B|A)=\frac{P\text{(A and B)}}{P(A)}`, where,

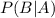`P(B|A)` = The probability of B given A.

Upon substituting our given values in above formula we will get,

`\text{P(Swim}|{\text{bridge)}=\frac{\text{P(The members play bridge and swim)}}{P(\text{The members play bridge)}}`

`\text{P(Swim}|{\text{bridge)}=(0.73)/(0.82)`

`\text{P(Swim}|{\text{bridge)}=0.890243902439`

`\text{P(Swim}|{\text{bridge)}\approx 0.89`

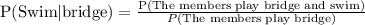
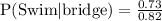
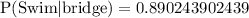
Therefore, the probability that the member swims, given that the member plays bridge is 0.89.

Answer 2

p(swim | bridge) = p(swim & bridge)/p(bridge)
.. = 0.73/0.82
p(swim | bridge) ≈ 0.89