Question

Is △DBE similar to △ABC ? If so, which postulate or theorem proves these two triangles are similar?

A. △DBE ​ is similar to ​ △ABC ​ by the ​ SAS Similarity Theorem ​
B. △DBE ​ is similar to ​ △ABC ​ by the ​ SSA Similarity Theorem ​
C.​ △DBE ​ is similar to ​ △ABC ​ by the ​ SSS Similarity Theorem ​
D. △DBE ​ is not similar to ​ △ABC

Answer 1

DBE is similar to ABC by the SAS Similarity Theorem

Answer 2

Explanation:

In the given figure we have two triangles (One into another).

In triangle BDE,

`DB=10\ cm`

`BE=16\ cm`

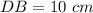
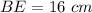
In triangle ABC,

`AB=BD+AD=10+15=25\ cm`

`BC=CE+EB=24+16=40\ cm`

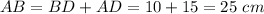
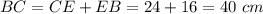
Now, in ΔABC and ΔBDE , we have

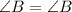`\angle{B}=\angle {B}` [Reflexive property]

`(BD)/(AB)=(10)/(25)=(2)/(5)=(16)/(40)=(BE)/(CE)`

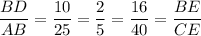
By SAS Similarity Theorem ​,

ΔDBE ​ is similar to ​ ΔABC ​

• SAS Similarity Theorem say that if two sides in a triangle are proportional to two sides in another triangle and the included angle in both are congruent then the two triangles are said to be similar.