Answer:
The temperature at which the rate of the reaction would be twice as fast as when the reaction runs at 730.6 K is 743.12 K.
Step-by-step explanation:
According to the Arrhenius equation,

![\log (K_2)/(K_1)=(E_a)/(2.303R)* [(T_2-T_1)/(T_1T_2)]](https://img.qammunity.org/2019/formulas/chemistry/college/2rmjtg6u1s0yacy2rgweiwwiqvzge206id.png)
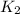 = rate of reaction at
= rate of reaction at
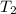
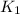 = rate of reaction at
= rate of reaction at
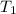
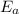 = activation energy
= activation energy
R = gas constant
We have:
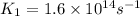
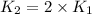
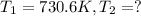
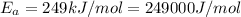
![\log (2K_1)/(K_1)=(249000 kJ/mol)/(2.303* 8.314 J/mol K)* [(T_2-730.6 K)/(730.6 K* T_2)]](https://img.qammunity.org/2019/formulas/chemistry/college/5lmkk7fznzziyk1hwmye0pzqe7uy9gyo27.png)
![0.3010=(249000 J/mol)/(2.303* 8.314 J/mol K)* [(T_2-730.6 K)/(730.6 K* T_2)]](https://img.qammunity.org/2019/formulas/chemistry/college/sfeh6hcj4a025p13yod50ldq6pquppwixf.png)
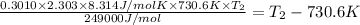
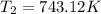
The temperature at which the rate of the reaction would be twice as fast as when the reaction runs at 730.6 K is 743.12 K.