Answer:
There is no minimum cost for the fencing that can satisfy these conditions.
as the equation obtained for this problem is y =
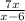 .
.
Explanation:
let length of the rectangular rose garden be x
and breath of the rectangular rose garden be y
then the area of the garden = xy
cost of fencing a foot for the 3 non road sides = $6
and cost of fencing a foot for a road side = $8
total cost of fencing = 6x + 8x + 6y + 6y
so, total cost = 14x + 12y
cost of fencing for every square foot of the area =$2
So, 2xy = 14x + 12y
=> 2xy = 14x + 12y
Also, x and y has to satisfy x>0 and y>0
You can solve for y (or x if you prefer)
2xy-12y=14x
xy - 6y = 7x
y(x-6)=7x
y =
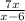
we can check that this function has no minimum value.
as we increase x (starting any x > 6 to make y positive) to make y minimal, y will decrease but the product xy will increase.
So, there is not a minimum cost for fencing that can satisfy these conditions.