Question

Determine the ratio in which the point (–6, m) divides the join of A(–3, –1) and B(–8, 9). Also, find the value of m.

Answer 1

m=5

Explanation:

Given: Point
`C(x_3,y_3)=(-6,m)` divides the join of point
`A(x_1,y_1)=(-3,-1)` and point
`B(x_2,y_2)=(8,9)`

Let the line AB divides by Point C in a ratio m:n=k:1

Then, Using section formula
`(x_3,y_3)=(x_1n+x_2m)/(m+n),(y_1n+y_2m)/(m+n)`

Applying formula,

`x_3,y_3=(x_1n+x_2m)/(m+n),(y_1n+y_2m)/(m+n)`

`x_3,y_3=(-8k-3)/(k+1),(9k-1)/(k+1)`

But,
`x_3=-6`

Therefore,
`x_3=(-8k-3)/(k+1)`

`-6=(-8k-3)/(k+1)`

`-6k-6=-8k-3`

`2k-3=0`

`k=(3)/(2)`

Therefore, C divides line AB in 3:2

Now,
`m=(9k-1)/(k+1)` where, k=3/2

`m=(9(3)/(2)-1)/((3)/(2)+1)`

`m=((25)/(2))/((5)/(2))`

`m=(25*2)/(2*5)`

`m=5`

Answer 2

Ratio = 3 : 2 and value of m = 5.

Explanation:

We are given the end points ( -3,-1 ) and ( -8,9 ) of a line and a point P = ( -6,m ) divides this line in a particular ratio.

Let us assume that it cuts the line in k : 1 ratio.

Then, the co-ordinates of P =
`( (-8k-3)/(k+1),(9k-1)/(k+1) )`.

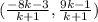But,
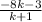`(-8k-3)/(k+1)` = -6

i.e. -8k-3 = -6k-6

i.e. -2k = -3

i.e.
`k = (3)/(2)`

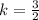
So, the ratio is k : 1 i.e
`(3)/(2) : 1` i.e. 3 : 2.

Hence, the ratio in which P divides the line is 3 : 2.

Also,
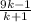`(9k-1)/(k+1)` = m where
`k = (3)/(2)`

i.e. m =
`((9 * 3)/(2)-1)/((3)/(2)-1)`

i.e. m =
`(27-2)/(3+2)`

i.e. m =
`(25)/(5)`

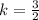
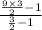
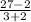
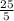
i.e. m = 5.

Hence, the value of m is 5.