Answer:

Explanation:
There's a very useful pattern in factoring and multiplying binomials called a difference of squares, and it looks like this:

We can use this difference of squares to factor the expression we've been given, setting
 and
and
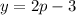 to obtain the expression
to obtain the expression
![(2p+3)^2-(2p-3)^2=[(2p+3)+(2p-3)][(2p+3)-(2p-3)]](https://img.qammunity.org/2019/formulas/mathematics/college/fuphtmo6m7mrq2a6sut87jqc7044eoiz0d.png) (1)
(1)
tackling each of the multiplicands on the right:
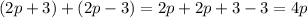 (Left)
(Left)
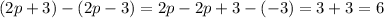 (Right)
(Right)
This simplifies the expression on the right of (1) to
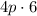 , or simply
, or simply
 .
.