Question

2) Line segment MK has endpoints at (2, 3) and (5, ?4). Segment M'K' is the reflection of MK over the y-axis. Which statement describes the relationship between MK and M'K'? A)M'K' is twice the length of MKB)M'K' is half the length of MK.C)M'K' is the same length as MK.D)More information is needed to determine the relationship

Answer 1

M'K' is the same length as MK.

Explanation:

A reflection is a rigid transformation. Rigid transformations do not affect the length of the line segment

Answer 2

Option C -M'K' is the same length as MK

Explanation:

Given : Line segment MK has endpoints at (2, 3) and (5,4)

M'K' is the reflection of MK over the y-axis

By definition of reflection: reflection of point (x,y) across the the y-axis is the point (-x,y)

which implies M'K' has end points (-2,3) and (-5,4)

Now, we find the length of MK

let
`(x_1,y_1)=(2,3)\\\\(x_2,y_2)=(5,4)`

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

⇒
`d=√((2-5)^2+(4-3)^2)`

⇒
`d=√(9+1)`

⇒
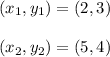
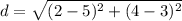
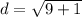
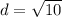`d=√(10)` ....(1)

Now, we find the length of M'K'

let
`(x_1^('),y_1^('))=(-2,3)\\\\(x_2^('),y_2^('))=(-5,4)`

`d^(')=\sqrt{(x_2^(')-x_1^('))^2+(y_2^(')-y_1^('))^2}`

⇒
`d^(')=√((-2+5)^2+(3-4)^2)`

⇒
`d^(')=√(9+1)`

⇒
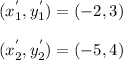
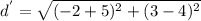
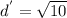`d^(')=√(10)` .....(2)

from (1) and (2) we simply show that the length of MK and M'K' is equal

we can also refer the figure attached for reflection of MK and M'K'

therefore, Option C is correct