Question

Identify the type of sequence shown in the table below and select the appropriate response. (5 points)

n f(n)
1 12
2 −36
3 108
4 −324
5 972

Answer 1

Its geometric as you are multiplying by -3 each time

Answer 2

The given sequence is geometric, which reason is -3.

Explanation:

If we pay attention to the sequence, we would observe that
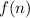`f(n)` is increasing by a reason of
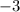`-3`, because

`12(-3)=-36\\-36(-3)=108\\108(-3)=-324\\-324(-3)=972`

So, basically, each term is being multiplied by
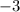`-3`, that's what makes the sequence, which is a geometric sequence, because it's being built by a factor, that is, a number which multiplies each term.

When you have to deduct if you have a arithmetic sequence or a geometric sequence, you need to observe if such sequence is increasing or decreasing faster. Like this case, you can see that the numbers are increasing rapidly, that means it's built based on a factor, not a difference, because when we use a difference to form a sequence, that will grow slower and it would be an arithmetic sequence.

Therefore, the given sequence is geometric, which reason is -3.