Question

Write the equation of a line in slope intercept form that is parallel to 2x + 4y = 10 and passes through the point (8, 2).

A) 16x + 8y = 10


B) y = −12x + 6

C) y = −12x+2

D) y=8x + 2

Answer 1

y = -1/2 x + 6

Explanation:

2x + 4y = 10

4y = -2x + 10

y = -1/2 x + 5/2

Parallel lines, slope is the same = -1/2

passes through the point (8, 2) so

y - 2 = -1/2(x - 8)

y - 2 = -1/2 x + 4

y = -1/2 x + 6

Answer 2

y = -1/2x + 6

Explanation:

We know that the slope intercept form of a line is
`y=mx+c`.

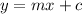Also, if two lines are parallel, they have the same slope. So re-writing the given equation 2x + 4y = 10 in the slope intercept form to find know its slope.

`2x + 4y = 10\\\\4y=-2x+10\\\\y=(-2)/(4) +(10)/(4)\\ \\y=(-1)/(2) +(10)/(4)`

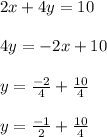
So the slope of the equation will be
`-(1)/(2)`.

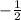Finding the y-intercept (c):

`y=mx+c\\\\2=-(1)/(2) (8)+c\\\\c=6`

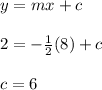
Therefore, the equation of the line n slope intercept form that is parallel to 2x + 4y = 10 and passes through the point (8, 2) is y = -1/2x + 6.