Question

Devante is proving that perpendicular lines have slopes that are opposite reciprocals. He draws line m and labels two points on the line as (a, 0) and (0, b) . Enter the answers, in simplest form, in the boxes to complete the proof. The slope of line m is . Rotate line m 90° clockwise about the origin to get line n. The labeled points on line m map to (0, −a) and (, ) on line n. The slope of line n is . The slopes of the lines are opposite reciprocals because the product of the slopes is .

Answer 1

The slope of line m is (-b/a).

The labelled points on line m map to (0,-a) and (b,0) on the line n.

The slope of line n is (a/b).

The slopes of the lines are opposite reciprocals because the product of the slopes is -1.

Explanation:

The slope of a line connecting the points (x₁,y₁) and (x₂,y₂) is

`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

The slope of line m is

`m_(1) = (b-0)/(0-a) = - (b)/(a)`

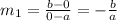
The line is rotated clockwise by an angle 90° to get line n.

The coordinates of the line n are (0,-a) and (b,0)

The slope of line n is

`m_(2) = (0+a)/(b-0) =(a)/(b)`

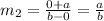
We see that,

m₁m₂ = -(b/a) * (a/b) = -1

Hence the products of the slopes of perpendicular lines is -1.