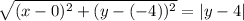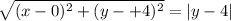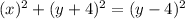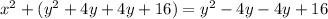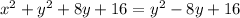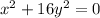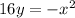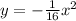Question

Derive the equation of the parabola with a focus at (0, −4) and a directrix of y = 4.

Answer 1

Answer: f(x)=-1/16 x^2

Answer 2

`y=-(1)/(16) x^2`

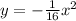
Explanation:

Equation of parabola with focus at (0,-4) and directrix is
`y=4`.

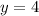We know that parabola is the locus of all the points such that the distance from fixed point on the parabola to fixed line directrix is the same.

The parabola is opening downwards.

Let any point on parabola is (x,y).

Distance from focus(0,-4) to (x,y) =
`√((x-0)^2+(y-(-4))^2)=|y-4|`

`√((x-0)^2+(y-+4)^2)=|y-4|`

`(x-0)^2+(y+4)^2=(y-4)^2`

`(x)^2+(y+4)^2=(y-4)^2`

`x^2+(y^2+4y+4y+16)=y^2-4y-4y+16`

`x^2+y^2+8y+16=y^2-8y+16`

`x^2+16y^2=0`

`16y=-x^2`

`y=-(1)/(16) x^2`