Question

Bill Ding plans to build a new hardware store. He buys a rectangular lot that is 50 ft by 200 ft, the 50-ft dimension being along the street. The store is to have 4000 ft2 of floor space. Construction costs $100 per linear foot for the part of the store along the street and only $80 per linear foot for the parts along the sides and back. To what dimensions should Bill build the store to minimize construction costs

Answer 1

Length a = 59.62

Width b = 67.09

Cost = $10,734.4

Explanation:

Solution:

Let a be the length and b be the width.

Area of the rectangle = a x b

a x b = 4000

Cost of the construction:

Cost = 100a + 80(a + 2b)

Cost = 100a + 80a + 160b

Cost = 180a + 160b Equation of the Cost of the construction.

Now, we need a and b to calculate the minimum cost required to build a lot.

From the area = a x b

we have,

a x b = 4000

b = 4000/a

Putting this equation into the cost of the construction.

We get:

Cost = 180a + 160 x (4000/a)

Cost = 180a + 640000/a

Differentiating with respect to a, we get

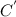`C^(')` = 180 - 640000/
`a^(2)`

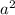
Putting
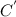`C^(')` = 0

180 - 640000/
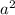`a^(2)` = 0

Taking LCM

180
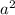`a^(2)` - 640000 = 0

Solving for a

180
`a^(2)` = 640000

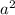`a^(2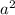)` = 640000/180

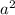`a^(2)` = 3555.55

Taking square root

a = 59.62

As we know,

b = 4000/a

putting the minimum value of a = 59.62

b = 4000/59.62

b = 67.09

So, now we have both the dimensions a and b

Putting the values of a and b we will get the cost of the construction.

Cost = 180a + 160b

Cost = 180(59.62) + 160(67.09)

Cost = $10,734.4

Hence, $10,734.4 will be the minimum cost of the construction for Bill Ding.