Question

Solve the system of linear equations. (Enter your answers as a comma-separated list. If there is no solution, enter NO SOLUTION. If the system has an infinite number of solutions, express x1, x2, and x3 in terms of the parameter t.)

Answer 1

The solution can be defined as follows:

Explanation:

Augmented matrix for the given system is

`\left[\begin{array}{ccccc}2&1&-2&|&4\\4&0&2&|&10\\ -4&5&-17&|&-15 \end{array}\right]`

Apply elementary row transformations on the matrix:

`R_1\to R_2 (2) \sim \left[\begin{array}{ccccc}4&2&-4&|&8\\4&0&2&|&10\\ -4&5&-17&|&-15 \end{array}\right] \\\\\\R_2\to R_2-R_1\\R_3\to R_3 (1)/(7) \sim \left[\begin{array}{ccccc}4&2&-4&|&8\\0&-1&3&|&1\\ 0&1&-3&|&-1 \end{array}\right] \\\\R_3\to R_3+R_2 \sim \left[\begin{array}{ccccc}4&2&-4&|&8\\0&-1&3&|&1\\ 0&0&0&|&0 \end{array}\right]`

Matrix Ranking = 2 = Matrix Ranking So the method in question is consistent

And there are endless options. To be the equation,

We're having

`\to 4x_1+2x_2-4x_3=8 ..........(1)\\\\ \to -x_2+3x_3=1............(2)\\\\take\ x_3=s`

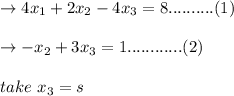
from equation 2 we get
`-x_2+ 3s = 1`

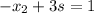
Substituting
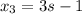`x_3= 3s- 1`in equation 1 we get

`\to 4x_1 +6s-2-4s=8 \\\\\to 4x_1=-2s+10\\\\\to x_1=-(1)/(2)s+(5)/(2)`

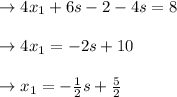
`\left[\begin{array}{c}X_1\\x_2\\x_3\end{array}\right]= \left[\begin{array}{c}-(1)/(2)s +(5)/(2) \\3s-1\\s\end{array}\right]`