Answer:
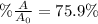
Step-by-step explanation:
Hello!
In this case, since the kinetics of the radioactive decay is assumed to be first-order, it is possible to use the following equation to quantify that change:
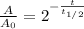
Thus, given the elapsed time, 635 years, and the half-life, 1599 years, we can compute the fraction of the present amount:
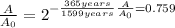
Thus, the percent is:
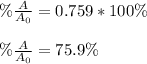
Best regards!