Question

Identify the focus and directrix of the parabola whose equation is (y-4)^2 = -12(x-7)

Answer 1

Answer : Focus (4,4) , directrix x=10

Answer 2

Answer : Focus (4,4) , directrix x=10

Given equation is

`(y-4)^2 = -12(x-7)`

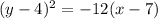
The given equation is in the form of

`(y-k)^2 = 4p(x-h)`

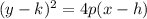
Where vertex is (h,k)

h = 7 and k = 4 so vertex is (7,4)

4p = -12 so p = -3

Focus is (h+p, k)

h=7, k=4 and p = -3

focus is (7-3, 4) that is (4,4)

now we find directrix

Directrix x= h-p

So x= 7-(-3)= 10

Focus (4,4) , directrix x=10