Question

For quadrilateral GHIJ to be a parallelogram, what needs to be congruent to JGH and GHI

A) IJK, HJK

B) GKJ, HKI

C) JIH, GJI

D) HGJ, GJI

Answer 1

Answer: The correct option is C.

Step-by-step explanation:

It is given that GHIJ is a quadrilateral and HJ, GI are the diagonals of the quadrilateral.

Let GHIJ is a parallelogram.

The opposite sides of the parallelogram are parallel and have same length. The diagonals divides the parallelogram in two equal or congruent parts. Diagonal bisects the angle.

Since JH is a diagonal so triangle JGH and JIH are congruent because,

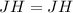`JH=JH` (common side)

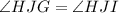`\angle HJG=\angle HJI` (JH bisects the angle J)

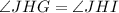`\angle JHG=\angle JHI` (JH bisects the angle H)

So by ASA rule of congruence triangle JGH and JIH are congruent.

Since GI is a diagonal so triangle GHI and GJI are congruent because,

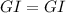`GI=GI` (common side)

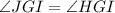`\angle JGI=\angle HGI` (GI bisects the angle G)

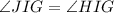`\angle JIG=\angle HIG` (GI bisects the angle I)

So by ASA rule of congruence triangle GHI and GJI are congruent.

If these triangle are congruent to each other then the we can say that the quadrilateral is a parallelogram.

So, the correct option is C.