Denote the area of quadilateral MBQP as A, the area of the triangle MBP as
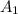 and the area of the triangle BPQ as
and the area of the triangle BPQ as
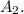
Note that:
1.
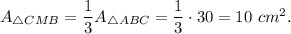
2.
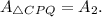
3.
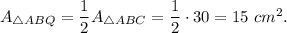
4.
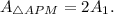
Now


You get the system of three equations:
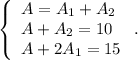
Substitute the first equation into the last two:
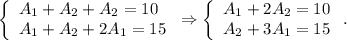
From the first equation
 and then
and then
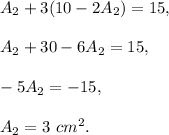
Thus,
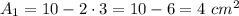
and

Answer: 7 sq. cm