Question

The number of customers who ate at a fast food restaurant between 1:00 P.M. And 3:00 P.M. Each day last week are listed here: 55, 37, 52, 50, 33, 46, 53 What's the standard deviation of the data set?

Answer 1

Standard deviation of the data set = 7.84

Explanation:

To calculate the standard deviation of the data set first we take the mean of the data .

Mean =
`((55+37+52+50+33+46+53))/(7)`

=
`(326)/(7)`

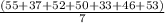
= 46.57

Now we subtract the mean from data set and square the answer.

55 - 46.57 = 8.43² = 71.06

37 - 46.57 = -9.57² = 91.58

52 - 46.57 = 5.43² = 29.48

50 - 46.57 = 3.43² = 11.76

33 - 46.57 = -13.57² = 184.14

46 - 46.57 = -0.57² = 0.32

53 - 46.57 = 6.43² = 41.34

Then we will take the mean of squared result.

`((71.06+91.58+29.48+11.76+184.14+0.32+41.34))/(7)`

=
`\frc{429.68}{7}`

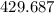
Variance = 61.38775509

Lastly take the square root of variance

=
`√(61.38775509)`

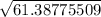
= 7.835033828 rounded to 7.84

Standard deviation of the data set = 7.84

Answer 2

The standard deviation is
`7.8` correct the nearest tenth.

EXPLANATION

The data set given to us is
`55,37,52,50,33,46,53`.

The standard deviation of the given data set can be calculated using the formula,

`Standard\:deviation=\sqrt{((x-\bar X)^2)/(n) }`

where
`\bar X=(\sum x)/(n)`

`\bar X=(55+37+52+50+33+46+53)/(7)`

`\bar X=(326)/(7)`

`\bar X=46.57`

We now find the standard deviation as follows;

`SD=\sqrt{( (55-46.57)^2+(37-46.57)^2+(52-46.57)^2+(50-46.57)^2+(33-46.57)^2+(46-46.57)^2+(53-46.57)^2 )/(7) }`

`Standard\:deviation=\sqrt{(71.06+91.58+29.48+11.76+184.14+0.32+41.34)/(7) }`

`Standard\:deviation=\sqrt{(429.68)/(7) }`

`Standard\:deviation=√(61.38)`

`Standard\:deviation=7.84`