The answer is:
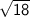
Work/explanation:
What are irrational numbers?
An irrational number is a number that cannot be expressed in the form of p/q, where q ≠ 0.
Note that terminating decimals are NOT irrational numbers.
So the first one is not an irrational number.
Let's consider the next one -
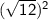
The square root and the square cancel each other out, and what is left is 12, which is a perfectly rational number.
Now we consider choice C, which is
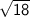 .
.
This one is an irrational number, as it cannot be expressed in p/q form.
Finally, let's consider choice D.
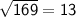 , which is rational too!
, which is rational too!
Hence,
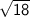 is irrational.
is irrational.