Answer::
Givens
Store A's price is
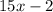
Store B's price is

Where
 represents the number of items.
represents the number of items.
Now, observe that the coefficient of both expressions is 15, because
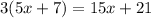
Remeber that the coefficient of the x-variable is always the constant rate of change. Also, the given expressions can be expressed as linear functions
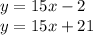
Observe that both Stores have already the same rate, which is 15.
Therefore, they have the same rate at any number of items dry cleaned.
What they have different is their initial condition, -2 and 21 respectively, but the rate is the same.