Line AB and CD have the following points: A(2, 4), B(9, 8), C(-1, 2), and D(3, -5). Are the lines parallel, perpendicular, or neither? Perpendicular Neither Parallel

Question

asked Jan 24, 2019 125k views

2 Answers

AdityaSrivast · Answer 1 · 2019-01-31T06:36:02+0000

We are given coordinates of A, B, C and D :

A(2, 4), B(9, 8), C(-1, 2), and D(3, -5).

Now, we need to find the slopes of AB and CD.

Slope of AB is :

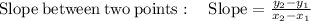
$\mathrm{Slope\:between\:two\:points}:\quad \mathrm{Slope}=(y_2-y_1)/(x_2-x_1)$

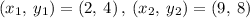
$\left(x_1,\:y_1\right)=\left(2,\:4\right),\:\left(x_2,\:y_2\right)=\left(9,\:8\right)$

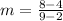
m=(8-4)/(9-2)

m=(4)/(7) .

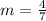Slope of CD is:

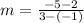
$m=(-5-2)/(3-\left(-1\right))$

m=-(7)/(4) .

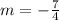Slope of CD is negative reciprocal of slope of slope of AB.