The point (- square-root 2/2, square-root2/2 is the point at which the terminal ray of angle theta intersects the unit circle. What are the values for the cosine and cotangent f…

Question

asked Jun 16, 2019 36.6k views

2 Answers

Svenningsson · Answer 1 · 2019-06-22T19:02:57+0000

Answer: The value of cosine is
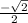$\frac{-√(2)} {2}$ and the value of cotangent is -1.

Step-by-step explanation:

The given point is
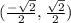$(\frac{-√(2)} {2}},\frac{√(2)} {2})$ .

Since the x coordinate is negative and y coordinate is positive so the point must be lies in second quadrant.

The distance of the point from the origin is,

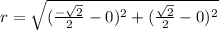
$r=\sqrt{(\frac{-√(2)} {2}-0)^2+(\frac{√(2)} {2}-0)^2}$

$r=\sqrt{ (2)/(4)+(2)/(4)}$

r=1

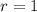
The given point is in the form of (a,b). So we get,

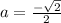
$a=\frac{-√(2)} {2}$

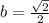
$b=\frac{√(2)} {2}$

The formula for cosine,

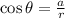
$\cos \theta =(a)/(r)$

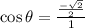
$\cos \theta =\frac{\frac{-√(2)} {2}}{1}}$

$\cos \theta =\frac{-√(2)} {2}}$

The formula for cotangent,

$\cot \theta =(a)/(b)$

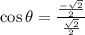
$\cos \theta=\frac{\frac{-√(2)} {2}}{\frac{√(2)} {2}}$

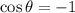
$\cos \theta=-1$

Therefore, the value of cosine is
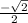$\frac{-√(2)} {2}$ and the value of cotangent is -1.