Question

The distance between the origin when a number and point representing the real number

Answer 1

1. In one Dimension

Draw any line , mark O, to represent center i.e origin and mark two points a and b on opposite side of O, where a and b are any two real number.

then,
`|a| =a,{\text{for example if a =5.6, then}} |5.6|=|5.6| , |b|=b {\text{for example, if b=-9.2, then}} |-9.2|=|9.2|`

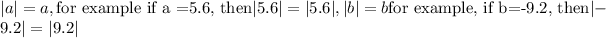
2. In two dimension

Origin,O =(0,0), A point in any of four quadrants=A(x,y),B(-x,y),C(-x,-y),D(x,-y).

Then , OA =OB=OC=OD=
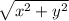`\sqrt{x^(2)+ y^(2)`, where x, y are any two same or distinct real number.