Question

Use remainder theorem to find the remainder when the function f(x) = x^3 + 8x^2 - 2x is divided by (x+3)

Answer 1

The correct option is 3.

Explanation:

According to the remainder theorem, if a polynomial P(x) is divided by (x-c), then the remainder is equal to P(c).

The given function is

`f(x)=x^3+8x^2-2x`

Using the remainder theorem, the remainder when the function f(x) is divided by (x+3) is equal to f(-3). The remainder is

`f(-3)=(-3)^3+8(-3)^2-2(-3)`

`f(-3)=-27+8(9)+6`

`f(-3)=-27+72+6`

`f(-3)=-27+78`

`f(-3)=51`

The remainder is 51. Therefore the correct option is 3.

Answer 2

f(x) = x^3 + 8x^2 - 2x is divided by (x+3)

When a polynomial function f(x) divided by (x-a), then remainder is f(a)

Given that f(x) divide by (x+3)

First we set x+3 =0 and solve for x

x+3 =0 so x=-3

Now plug in -3 for x in f(x) and find out f(-3)

f(-3) is the remainder

`f(x) = x^3 + 8x^2 - 2x`

`f(-3) = (-3)^3 + 8(-3)^2 - 2(-3)= -27 +72+6 = 51`

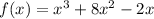
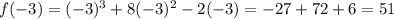
Remainder is 51

Answer is 51