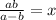Question

1/x + 1/a = 1/b solve for x

Answer 1

Steps:

Firstly, we want it so that the denominators of all the fractions are the same. To do this, we must find the LCD, or lowest common denominator of each denominator. To do that, since they are all variables multiply them together to get abx.

Now that we have the LCD, multiply 1/x by ab/ab, 1/a with bx/bx, and 1/b by ax/ax:

`(1)/(x)* (ab)/(ab) =(ab)/(abx)\\\\(1)/(a)* (bx)/(bx)=(bx)/(abx)\\\\(1)/(b)* (ax)/(ax)=(ax)/(abx)\\\\\\(ab)/(abx)+(bx)/(abx)=(ax)/(abx)`

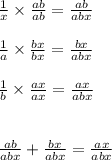
Now that they have the same denominator, multiply both sides by abx:

`ab+bx=ax`

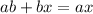
Next, subtract bx on both sides:

`ab=ax-bx`

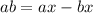
Next, factor out x on the right side:

`ab=(a-b)x`

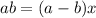
Lastly, divide both sides by a - b:

`(ab)/(a-b)=x`

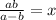
Answer:

In short, your answer is
`(ab)/(a-b)=x`