ANSWER
The remainder is

Step-by-step explanation
Let
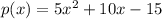
We shall apply the remainder theorem to obtain the remainder when
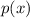
is divided by

According to the remainder theorem, if a polynomial
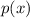
is divided by
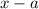
then the remainder is

So we set
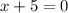
and solve for

to obtain,

We now substitute -5 into the given polynomial to find the remainder.
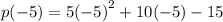
This gives us,

This will simplify to,
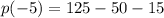
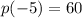
Therefore the remainder is
