Question

A restaurant sells 330 sandwiches each day. For each $0.25 decrease in price, the restaurant sells about 15 more sandwiches. How much should the restaurant charge to maximize daily revenue? What is the maximum daily revenue? Each sandwich is 6$ beforehand...

Answer 1

The value that optimizes this inequality is x = 1, since it represents the vertex of the parabola. Therefore, $ 0.25 is the price that must be discounted to maximize revenues

With x = 1 the value of the new income will be = $ 1983.75

Explanation:

Revenue with the current sale price is:

6 * 330 = $ 1980

Let's call x the number of times the price of a sandwich decreases, that is, if x = 1 then the price of the sandwich decreases by $ 0.25

Then, the price would be:

Price = (6-0.25x)

Then, if the price is decreased by a factor of x, then the number of sandwiches sold will increase by a factor of 15x. Therefore the number of clients will be:

Sale = (330 + 15x)

Now we need an equation for income. The income will be equal to the sale price, for the number of sandwiches sold

Income = price * sale

Income = (6-0.25x) (330 + 15x)

In order for this restaurant pricing model to be profitable, the revenues with the new sale price must be greater than the revenues with the sale price of $ 6. So:

New income> current income.

`(6-0.25x) * (330 + 15x)> 330 * 6\\ (6-0.25x) * (330 + 15x)> 1980`

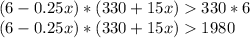
The left side of the inequality represents a parabola:

`-3,750x ^ 2 + 7.5x + 1980> 1980`

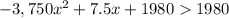
The value that optimizes this inequality is x = 1, since it represents the vertex of the parabola. Therefore, $ 0.25 is the price that must be discounted to maximize revenues

The attached image shows the region that satisfies the proposed inequality and the vertex of the parabola:

`x = (-b)/(2a)`

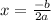
With x = 1 the value of the new income will be = $ 1983.75