slope = - 2, midpoint = (2, - 2 )
the slope m is calculated using the ' gradient formula '
m = ( y₂ - y₁ ) / (x₂ - x₁ )
with (x₁, y₁ ) = (4, - 6 ) and (x₂, y₂ ) = (0, 2 )
m =
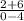 =
=
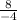 = - 2
= - 2
calculate midpoint using midpoint formula
{
 (4 + 0 ),
(4 + 0 ),
 (- 6 + 2 )] = (2, - 2 )
(- 6 + 2 )] = (2, - 2 )
gradient of perpendicular bisector = -
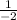 =
=

equation in slope-intercept form is
y = mx + c ( m is slope and c the y-intercept )
partial equation is y =
 x + c
x + c
to find c substitute ( 2, - 2) into the partial equation
- 2 = 1 + c ⇒ c = - 3
y =
 x - 3 in slope-intercept form
x - 3 in slope-intercept form