Question

A toy company has determined that the revenue generated by a particular toy is modeled by the following equation: 10x - 0.025x² The variable x is measured in thousands of toys produced, and r(x) is measured in thousands of dollars. What is the maximum revenue the company can earn with this toy?

Answer 1

Maximum revenue = 1000 thousands of dollars.

Step-by-step explanation:

We have the revenue equation
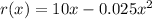`r(x)=10x - 0.025x^2`, where x is measured in thousands of toys produced, and r(x) is measured in thousands of dollars.

At maximum revenue the derivative of equation is zero

So,
`r'(x)=0\\ \\10 - 0.025*2x=0\\ \\ x=10/0.05\\ \\ x=1000/5=200`

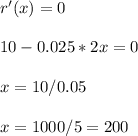
So maximum revenue is when 200 thousands of toys are produced.

Maximum revenue,
`r(200)=10*200 - 0.025*200^2\\ \\ r(200)=1000`

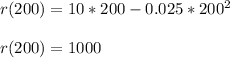
Maximum revenue = 1000 thousands of dollars.