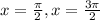Question

Here we will study the function f (x) = e ^ x sin (x), where x ∈ [0, 2π]. a) Determine where the function is decreasing and increasing. b) Find all local maximam and minimam. Does the absolute (global) maximam / minimam have? c) Determine where f (x) curves up and down. Also find any turning points.

Answer 1

we are given

`f(x)=e^x sin(x)`

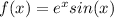
(a)

Firstly, we will find critical numbers

so, we will find derivative

`f'(x)=e^x sin(x)+e^x cos(x)`

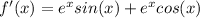
now, we can set it to 0

and then we can solve for x

we get

`x=(3\pi )/(4) ,x=(7\pi )/(4)`

now, we can draw a number line and then locate these values

and then we can find sign of derivative on each intervals

increasing intervals:

`[0,(3\pi)/(4) )U((7\pi)/(4) , 2\pi]`

Decreasing interval:

`((3\pi)/(4) ,(7\pi)/(4) )`

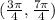
(b)

Local maxima:

It is the value of x where function changes from increasing to decreasing

so, local maxima is at

`x=(3\pi)/(4)`

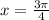
Local minima:

It is the value of x where function changes from decreasing to increasing

so, local minima is at

`x=(7\pi)/(4)`

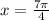
now, we will plug critical numbers and end values into original function

and we get

At x=0:

`f(0)=e^0 sin(0)`

`f(0)=0`

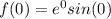
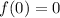
At
`x=(3\pi)/(4)`:

`f((3\pi)/(4))=e^{(3\pi)/(4)} sin((3\pi)/(4))`

`f((3\pi)/(4))=7.46049`

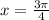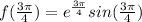
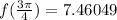
At
`x=(7\pi)/(4)`:

`f((7\pi)/(4))=e^{(7\pi)/(4)} sin((7\pi)/(4))`

`f((7\pi)/(4))=-172.640`

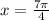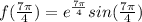
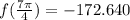
At
`x=2\pi`:

`f(2\pi)=e^(2\pi) sin(2\pi )`

`f(2\pi )=0`

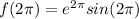
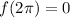
Global maxima:

It is the largest value among them

so, we get

`f((3\pi)/(4))=7.46049`

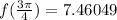
Global minima:

It is the largest value among them

so, we get

`f((7\pi)/(4))=-172.640`

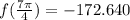
(c)

now, we can find second derivative

`f'(x)=e^x sin(x)+e^x cos(x)`

`f''(x)=(d)/(dx)\left(e^x\sin \left(x\right)+e^x\cos \left(x\right)\right)`

`=(d)/(dx)\left(e^x\sin \left(x\right)\right)+(d)/(dx)\left(e^x\cos \left(x\right)\right)`

`=e^x\sin \left(x\right)+\cos \left(x\right)e^x+e^x\cos \left(x\right)-e^x\sin \left(x\right)`

`f''(x)=2e^x\cos \left(x\right)`

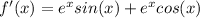
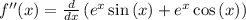
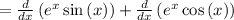
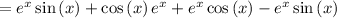
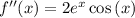
now, we can set it to 0

and then we can solve for x

`f''(x)=2e^x\cos \left(x\right)=0`

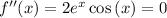
so, we get

`x=(\pi)/(2) ,x=(3\pi)/(2)`

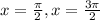
now, we can draw number line and locate these values

and then we can find sign of second derivative on each intervals

concave up intervals:

`[0,(\pi)/(2))U((3\pi)/(2), 2\pi]`

Concave down intervals:

`((\pi)/(2) ,(3\pi)/(2))`

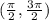
Turning points:

All values of x for which concavity changes

so, we get turning points at

`x=(\pi)/(2) ,x=(3\pi)/(2)`

Answer 2

fff

`f(x) = e^x sin (x)`

To find increasing and decreasing intervals we take derivative

`f'(x) = e^xsin(x)+e^x(cosx)= e^x(sinx+cosx)`

Now we set the derivative =0 and solve for x

`e^x(sinx+cosx)=0`

sinx + cosx =0

divide whole equation by cos x

`(sinx)/(cosx) + (cosx)/(cosx) =0`

tanx +1 =0

tanx = 1

`x=(3\pi )/(4)` and
`x=(7\pi)/(4)`

Now we pick a number between 0 to
`(3\pi )/(4)`

Lets pick
`(\pi )/(2)`

Plug it into the derivative

`f'(x) =e^{(\pi )/(2)}(sin((\pi)/(2))+cos((\pi )/(2)))`

= 4.810 is positive

So the graph of f(x) is increasing on the interval [0,
`x=(3\pi )/(4)`)

Now we pick a number between
`(7\pi)/(4)` to 2pi

Lets pick
`(11\pi)/(6)`

Plug it into the derivative

`f'(x) =e^{(11\pi)/(6)}(sin((11\pi)/(6))+cos((11\pi )/(6)))`

= 116 is positive

So the graph of f(x) is increasing on the interval
`((7\pi )/(4), 2\pi)`

Increasing interval is
`(0,(3\pi )/(4)) U ((7\pi )/(4), 2\pi)`

Decreasing interval is
`((3\pi)/(4), (7\pi)/(4))`

(b)

The graph of f(x) increases and reaches a local maximum at
`x=(3\pi)/(4)`

The graph of f(x) decreases and reaches a local minimum at
`x=(7\pi)/(4)`

(c)

f(0) = 0

`f(2\pi)=0`

`f((3\pi )/(4))=7.46`

`f((7\pi)/(4))=-172.64`

Here global maximum at
`x=(3\pi)/(4)`

Here global minimum at
`x=(7\pi)/(4)`