Question

Consider the parabola r​(t)equalsleft angle at squared plus 1 comma t right angle​, for minusinfinityless thantless thaninfinity​, where a is a positive real number. Find all points on the parabola at which r and bold r prime are orthogonal.

Answer 1

Given:-
`r(t)=< at^2+1,t>` ;
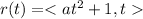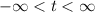`-\infty < t< \infty` , where a is any positive real number.

Consider the helix parabolic equation :

`r(t)=< at^2+1,t>`

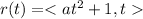
now, take the derivatives we get;

`r{}'(t)=<2at,1>`

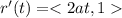
As, we know that two vectors are orthogonal if their dot product is zero.

Here,
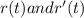`r(t) and r{}'(t)` are orthogonal i.e,
`r\cdot r{}'=0`

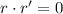
Therefore, we have ,

`< at^2+1,t>\cdot < 2at,1>=0`

`< at^2+1,t>\cdot < 2at,1>=<at^2+1\cdot\left(2at\right), t\cdot \left(1)>`

`=2a^2t^3+2at+t`

`2a^2t^3+2at+t=0`

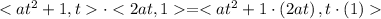
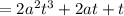
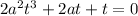
take t common in above equation we get,

`t\cdot \left (2a^2t^2+2a+1\right )=0`

⇒
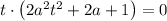
`t=0` or
`2a^2t^2+2a+1=0`

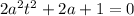
To find the solution for t;

take
`2a^2t^2+2a+1=0`

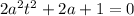
The number
`D = b^2 -4ac` determined from the coefficients of the equation
`ax^2 + bx + c = 0.`

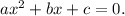
The determinant
`D=0-4(2a^2)(2a+1)`
`=-8a^2\cdot(2a+1)`

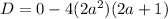
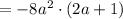
Since, for any positive value of a determinant is negative.

Therefore, there is no solution.

The only solution, we have t=0.

Hence, we have only one points on the parabola
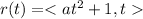`r(t)=< at^2+1,t>` i.e <1,0>