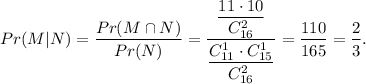You are given 16 teams, 11 have won at least one super bowl and 5 have not.
A. The probability that both selected teams have won at least 1 super bowl is

B. The probability that neither selected team has won at least 1 super bowl is
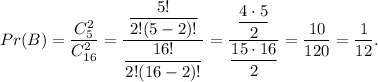
C. The probability that at least one selected team has won at least 1 super bowl is

D. to find the probability that the second team selected has won at least 1 super bowl given that the first team selected has not won a super bowl, consider such events:
P - the second team selected has won at least 1 super bowl;
Q - the first team selected has not won a super bowl.
Then

E. To find the probability that the second team selected has won at least 1 super bowl given that the first team selected has won at least 1 super bowl, consider events:
M - the second team selected has won at least 1 super bowl;
N - the first team selected has won at least 1 super bowl.
Then