The values of
 satisfying the compound inequality
satisfying the compound inequality
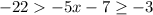 are
are
![\( x \in \left( -\infty, -(4)/(5) \right]\)](https://img.qammunity.org/2019/formulas/mathematics/middle-school/pzyeyyytcqo5xppaxtfzwhquw3o3enjq58.png) , indicating
, indicating
 is less than or equal to
is less than or equal to
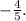
To find the values of
 that satisfy the compound inequality
that satisfy the compound inequality
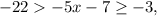 you can follow these steps:
you can follow these steps:
1. Isolate the variable
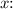
![\[ -22 > -5x - 7 \geq -3 \]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/oee15ptloipvo7onjbw5kibsdx2u7n59fq.png)
Add 7 to all parts of the compound inequality:
![\[ -15 > -5x \geq 4 \]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/sw98xti6kt27gzlsvu1so4nvnj336x0ytd.png)
Divide all parts by -5. Since you are dividing by a negative number, the direction of the inequality signs will change:
![\[ 3 < x \leq -(4)/(5) \]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/7ckth3pv39djqvqyjv38mlwqmodu7vnd2y.png)
2. Write the solution in interval notation:
![\[ x \in \left( -\infty, -(4)/(5) \right] \]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/fpn1fh7e2nrrrrye62x4yyu17qei51rzik.png)
This indicates that \( x \) can take any value less than or equal to
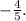
So, the answer is
![\( x \in \left( -\infty, -(4)/(5) \right] \).](https://img.qammunity.org/2019/formulas/mathematics/middle-school/hk3awwc0mkirnxp0m3i9hs55psyfiabg8c.png)
The probable question maybe:
What values of x satisfy the compound inequality −22 > −5x − 7 ≥ −3?