Question

"assume that s is a non-empty set of real numbers which is bounded above and lambda is the least upper bound. Prove that for all real numbers beta is less than lambda there is a real number alpha in s such that beta is less than alpha"

Answer 1

By definition, if
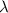`\lambda` is the least upper bound of the set
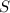`S`, it means two thing:

• 
  `\forall x \in S,\ x \leq \lambda`
• 
  `\forall \varepsilon>0,\ \exists x \in S:\ x>\lambda-\varepsilon`

In other words, the least upper bound of a set is greater than or equal to every single element of the set, but it is "close enough" to the elements of the set, because you guaranteed to find elements in the set between
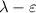`\lambda-\varepsilon` and
`\lambda`

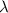
For example, pick
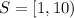`S = [1,10)`. Obvisouly, the least upper bound is
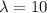`\lambda = 10`. In fact, every number in
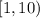`[1,10)` is smaller than 10, but as soon as you take away something from 10, say 0.01, you get 9.99, and there are elements in
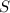`S` greater than 9.99, say 9.9999.

So, the claim is basically proven by definition: if
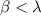`\beta < \lambda`, let
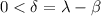`0 < \delta = \lambda - \beta`. By definition, there exists
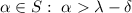`\alpha \in S:\ \alpha > \lambda - \delta`.